From County Boundaries to Satellite Orbits
with a Single Geopositioning Reference System
Hrvoje Lukatela,
Geodyssey Limited
http://www.geodyssey.com/
Paper presented at the SORSA/99 Symposium, Ottawa, August 1999)
Introduction
Hipparchus (the astronomer, 180-125 B.C.) was the first to
successfully use numbers and algebraic operations to define and
describe a spatial object larger than a land parcel. From his
time on, it was common to use planar computations for operational
systems dealing with local phenomena, and spherical or spheroidal
for the systems dealing with global phenomena.
Two millennia later, the algebra is carried out by electronic
devices, and there is an ever greater need to treat both local
and global phenomena in a single operational computer system -
and thus in a single computational frame of reference.
Hipparchus (the software product) represents an emerging class
of computational devices which no longer restrict the numerical
modeling of spatial objects - whether global or local - to planar
coordinate systems. In doing so, it offers system builders
the tools required to integrate seamlessly all possible classes of
spatial objects in a single computational frame of reference.
This is achieved by numerically representing the global location of
a point not by the common latitude and longitude in angular measure,
but by using three direction cosines instead. It is however important to
note that the geometry object thus represented is the same one as that
which is represented by latitude and longitude: the spatial direction of
the normal to the ellipsoidal surface.
Another important element that lies at the heart of every computer
system which manipulates large external collections of geographical
data is the schema by which a surface on which the data resides is
subdivided. Such subdivision is typically used for two important
purposes: to retrieve from the external storage only those data items
that are of use in a given context (for instance, create a graphical
view of a small locale within the total data area), but also to restrict
the amount of data that must be processed in order to derive a given
spatial algebra production.
In the Hipparchus system, this subdivision is based on the spheroidal
equivalent of a planar Voronoi tessellation. A detailed description
of both essential elements (i.e., global geographical coordinate
manipulation using direction cosines and a spheroidal Voronoi
tessellation) is available from a web-resident publication titled:
Hipparchus Geopositioning Model: an Overview.
The SORSA '99 symposium presentation was centered on an interaction of two
particular computational elements of the Hipparchus software tool: an
external representation of a collection of two-dimensional terrestrial
objects ("regions") and on Hipparchus orbit modeler.
Region collections
Hipparchus "region collection" is an organized external file containing
a spatial definition of a potentially large number of regions ("collection
members"). An application program can use such a file to find answers to a
number of practical questions, such as:
What is the order and location of a member's boundary vertices? Which parts of a screen window represent some member's interior? Is a given point inside or outside a given collection member? Which member or members have a given point inside them?
As the last proposition implies, a collection of regions is not
a "categorical classification" schema; i.e., members can overlap,
so that any point of the spheroidal surface can be inside more than
one member. (It is worth noting here, that in many instances, an
application designer's assumption that a given category of objects
are by definition non-overlapping needs to be re-addressed during
the life-cycle of the system: for instance, different high-order
political entities claiming the same territory).
A region collection file is divided into three parts:
index tables, a member structure definition and the coordinate
repository. Index tables provide a fast mechanism for both principal
searches: for an unknown member identifier from a known location,
and for the unknown location-defining data from a given member
identifier. The structure describes the relationship of a member
and a set of Voronoi cells. The coordinate repository consists of
all boundary vertices of all the collection members, given in
local (cell) coordinates. It represents the majority of the data
volume in the collection. This section is stored in cell order,
so that - as much as possible when a multi-dimensional surface
is mapped into a single dimension of file addresses - vertices
that are near-by on the ground remain near-by in the disk file.
In most computing environments such an arrangement results in
faster external data access.
Finally, it should be noted that regions represented in the
collection can be of any level of topological complexity (i.e., their
boundary can consist of any number of rings, with an unrestricted level of
"voids"), as long as the boundary rings do not cross each other, and
as long as the condition of topological consistency of the ring directions
is preserved.
Hipparchus orbit modeler
In order to provide the computing facilities necessary for
fast and high-volume correlation of terrestrial data (such as,
for instance, the members of a region collection described above)
and the visibility swath of a sensor mounted on an earth-orbiting
satellite, the Hipparchus software tool includes a third-order
orbit modeler. (Third-order is a term often used for orbit
modelers which include proper resolution of the time/position
relationship of an orbit of any degree of ellipsoidal
eccentricity, and includes both the precession and the
rotation of the apses). The orbit is defined by the classical
orbit parameter set.
The Hipparchus orbit modeler can return both the instantaneous
position of the satellite, as well as the elements of the external
orientation of the sensor. These can be used to intersect a
terrestrial object with the satellite nadir position (i.e., answer
the question: "what is the satellite over at a given time"), or
with the swath line (i.e., answer the question: "what does the
satellite "see" at a given time).
An example application
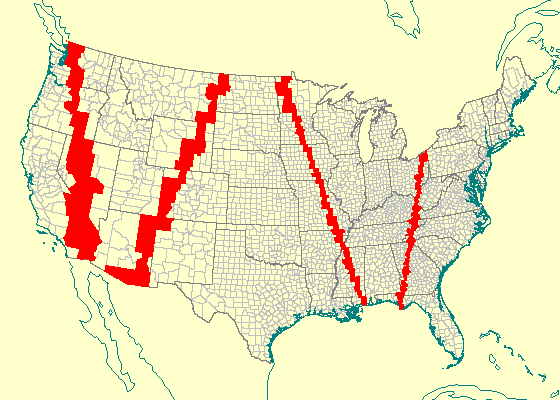
Fig. 1: Satellite nadir trace
The above picture is a single "frame" from an animated display
produced by the Hipparchus geographical "workbench" program called
Galileo. An extensive
User Guide for Galileo is available online; the program
is available - as a self-extracting archive - for free
download from Geodyssey's web server.
The image depicts a trace of a satellite nadir over a region
collection consisting of more than 3200 United States counties,
with more than 3.5 million boundary vertices. As the orbit modeler
produces updated satellite location data (at the orbit-time intervals
of 3 seconds) this is projected to the nadir point along the ellipsoid
normal. The point location thus obtained is used as a location argument
in a member search for the county over which the satellite is located.
The screen fill-area is than evaluated and applied to the map.
All the above computations are carried out with sub-millimetric
precision, inherent in the 64-bit direction cosine representation
of the positions returned by the orbit modeler as well as those
stored in the region collection file. The speed of computations
(on a 100 Mhz Pentium processor) is several orders of magnitude
above that of the orbit time passage.
Conclusion
The purpose of this presentation was to demonstrate primarily the
efficiency with which the direction cosine global coordinate manipulation
improves computational speed and precision. In addition, it provided
a graphical demonstration of the manner in which complex data
structures based on direction cosine coordinates (such as the Hipparchus
region collection file) can be used for fast spatial search and
visualization.
...
|