Hipparchus Geopositioning Model: an Overview
Hrvoje Lukatela,
Geodyssey Limited
http://www.geodyssey.com/
Paper presented at AUTO-CARTO 8, Baltimore, March 1987
Document URL: http://www.geodyssey.com/papers/hlauto8.html
Abstract
This paper introduces a novel digital geopositioning model. It is
based on computational geodesy in which direction cosines are used
instead of the conventional -angular- ellipsoid normal representation,
and eccentricity term expansions are replaced by iterative algorithms.
The surface is partitioned by a spheroid equivalent of the Voronoi
polygon network. The model affords seamless global coverage, easily
attainable millimetric resolution, and data-density sensitive location
indexing. Numerical representation of 0, 1 and 2 dimensional objects
is in complete accordance with the unbounded, spheroidal nature of
the data domain, free from any size, shape or location restriction.
Efficient union and intersection evaluations extend the utility of the
relational technique into the realm of geometronical systems with
non-trivial spatial precision requirements. Digital modelling of orbital
dynamics follows closely the numerical methodology used by terrestrial
geometry. The Hipparchus software package includes the
transformations and utility functions required for efficient generation
of transient graphics, and for the communication with systems based on
conventional cartographic projections.
Introduction
A numerical geopositioning model is an essential element of any system
wherein a dimension of space enters into the semantics of the
application - and therefore into the software technique repertoire - in a
fundamental way. It consists of location attribute data definitions
and computational algorithms, which allow position sensitive storage
and retrieval of data, and provide a basis for evaluation of spatial
relationships. (The term "spatial relationship" is used in this paper
to describe the formal statement of any practical spatial problem
which deals with positions of real or abstract objects on - or close
to - the Earth surface. Their nature can vary; examples might include
geodetic position computations, course optimization for navigation in
ice-infested waters or determination of the most probable location of
objects remotely sensed from a platform in the near Space.)
If the location attributes of data elements in a computer system are
used exclusively for the generation of a small-scale analog map
document, the demands made of a geopositioning model are few and
simple. When the area of coverage is limited, and projection
geometry, spatial resolution and partitioning of the data can be made
directly compatible with same characteristics of all future required
products, a single plane coordinate system is often employed. Such a
system is usually based on one of the large-area conformal projections
(e.g. Lambert, Gauss-Krueger, etc.), and provides adequate means to
identify positions, partition the data, and construct a location
index. The model may even allow limited spatial analysis.
However, with the increase of the area of coverage and the functional
power of information systems, the nature of the problem changes
considerably.
Precision requirements usually exceed the level of difference between
planar coordinate relationships and the actual object-space geometry.
In most cases, the generation of an analog map is reduced to a
secondary objective. Location attributes are primarily used to
support the evaluation of spatial relationships required by the
application. Indeed, as the volatility and volume of data grows, it
becomes increasingly common that a location-specific item enters a
system, contributes to the evaluation of a large number of spatial
relationships, and is ultimately discarded, without ever being
presented in the graphical form.
Even in systems used primarily to automate the production of analog
documents, there is often a need to accommodate many different
projection, resolution and data partitioning schemes on a continental
or even global scale.
A point is thus quickly reached where geopositioning model must
satisfy very demanding functional requirements, yet any restriction on
the data domain becomes unacceptable. From the application point of
view, the mapping from an atomic surface fraction into a distinct
internal numerical location descriptor must be global, continuous and
conjugate.
Faced with these requirements, manual spatial data processing resorts
to a combination of two techniques. A set of multiple planar
projection systems (e.g. UTM "zones") is used to achieve - seldom
successfully - the global coverage. Initially simple calculations are
cluttered with various "correction" terms in order to deal with
differences between planar coordinates and true object geometry.
A failure to understand the precise nature of spatial data
(especially, by ignoring the profound conceptual difference between an
analog map and the true data domain) often leads to a blind transplant
of conventional cartographic techniques into a computerized system.
This seldom results in a satisfactory geopositioning model:
cartographic projections are notorious for their computational
inefficiency; global coverage usually requires the use of
location-specific transformations. Programming becomes progressively
more complex as the precision requirements increase. Boundary
problems are difficult to solve; this imposes discontinuities or size
restrictions for the models of spatial data objects. Finally,
classical cartography offers little or no help in modelling of the
near-space geometry. The same system can therefore be forced to
employ two disparate numerical methodologies: one for the positions
on the Earth surface and quite another for orbital data. This
presents an increasingly serious problem in many emerging high
data-volume applications.
Design (or selection) criteria for a generalized location referencing
numerical model and software will change from one computerized
information system to another, but will be based - usually - on the
size of the area of interest, spatial resolution, anticipated data
volume, optimal computational efficiency, logical and geometrical
complexity of objects modelled, and on the level of precision with
which all these elements can be defined before the system is built.
Nevertheless, it is possible to list important functional requirements
that will pertain to a majority of extended coverage geographic
information systems:
-
Unrestricted numerical representation of arbitrarily-sized
and -shaped objects with 0, 1 and 2 dimensions (i.e. points,
lines, regions) relative to the surface of the Earth, and
efficient evaluation their unions and intersections.
-
Global coverage, without any regions of numerical instability
or deterioration; ability to precisely model spatial
relationships resulting from the unbounded, spheroidal nature
of the data domain.
-
Variable (application controlled!) levels of positional
resolution and computational geometry precision; up to
sub-millimeter level for location framework or field-measurement
related data.
-
High utilization level of the coordinate data-storage space.
-
Construction of data density and system activity level
sensitive surface partitioning and indexing scheme; capability
of dynamic re-partitioning in order to respond to a change in
density or activity pattern of an operational system.
-
Ability to effectively model the time/space relationships of
surface, aeronautical and orbital movements.
The quality of a generalized geopositioning model will obviously
depend not only on the extent to which the above criteria have been
satisfied, but on its software engineering potential as well. The
model must be capable of being implemented in program code which is
efficient, reliable, portable, and easily interfaceble to a large
number of different types of data-access services (i.e. file and
indexing schemes, database software packages e.t.c.) and application
problem-solving programs.
 Fig. 1: Hipparchus ellipsoid surface partitioning scheme
Fig. 1: Hipparchus ellipsoid surface partitioning scheme
The geopositioning model presented here consists of three key
components: a) spheroidal cell structure analogous to planar Voronoi
polygons; b) computational geodesy based on closed iterative
algorithms, and c) an unlabored representation of global ellipsoid
coordinates in terms of a cell identifier and description of location
within the cell. Since the computational bridge between the global
position and the location within the cell consists of a pseudo-
stereographic ellipsoid-plane transformation, Hipparchus has been
chosen as the name for the model. (Hipparchus, (180-125 B.C.) -
inventor of stereographic projection: the first truly practical
geopositioning model.)
The Hipparchus model provides a unique spatial framework,
and includes the algorithms necessary to encode data and evaluate spatial
relationships. In doing so, it attempts to satisfy - to the highest
extent possible - all the requirements mentioned above. The nature of
the framework and principles of its data manipulation techniques will
be examined next in some detail.
Global Ellipsoid Coordinates
A plane or sphere can be used to represent the surface of the Earth
only for limited-area, low-precision computations. A general purpose
geopositioning model will, however, require a better fitting surface.
Typically, a quadric, biaxial (rotational) ellipsoid is employed.
(Triaxial ellipsoid and various sets of polynomial correction terms to
a biaxial ellipsoid have both been employed in geodetic calculations
and proposed for general cartographic use. The discussion of
potential merits of those surfaces, and the ability of the proposed
model to accommodate them numerically, are beyond the scope of this
text.) The parameters of size and eccentricity of the reference
ellipsoid can be determined by a combination of theoretical
investigation into the equilibrium shape of a rotating near-liquid
body and terrestrial geometry and satellite orbit observations. This
is an open-ended process, resulting in occasional corrections of
ever-decreasing magnitude.
The position on the surface of the ellipsoid can be represented
numerically in many different ways. Conceptual clarity of the model,
as well as practical software engineering considerations, demand that
one such representation be used as a canonical form of global location
descriptor throughout the model. The selection of this numerical form
is one of the most critical decisions in the design of a
geopositioning model.
The traditional angular measurements of latitude and longitude are
extremely unsuitable for automated computations. Few, if any, spatial
problems can avoid multiple evaluations of trigonometric functions.
Moreover, convoluted programming techniques are often necessary to
detect areas of numerical instability and adjust an algorithm
accordingly. It would be simple to use Cartesian point coordinates
instead, but the domain would no longer be restricted to the ellipsoid
surface. An additional condition would have to be incorporated into
the statement of most surface-related geometry problems.
The geometrical entity described by latitude and longitude is a vector
normal to the surface of ellipsoid in the location thus defined. This
vector can be expressed by its direction cosines, and a normalized
triplet can be used as coordinates of a surface point. This appears
to be an ideal canonical location descriptor: the domain is restricted
to the surface; numerical manipulations based on vector algebra
productions are easy to program and simple to test, and a common
64-bit floating point numbers will yield sub-millimeter resolution
even at radial distances that are an order of magnitude above the
surface of the Earth.
Conventional formulae for the solution of ellipsoid geometry problems
were typically obtained by expansion in terms of an ascending power
series of eccentricity. While this was unavoidable for problems
lacking a closed solution, it was also often used in order to reduce
the number of digits which had to be carried in a numerical treatment
of a geodetic problem with a limited spatial extent. As long as the
eccentricity of the reference surface was constant, any a priori
precision criterion could be satisfied by either finding the maximum
value of the remainder dropped, or - more commonly - by deciding on
the threshold exponent beyond which terms could be ignored for a whole
class of practical problems.
Formulae thus obtained are useful for manual calculations but do not
provide a sound base for the construction of efficient and
data-independent computer algorithms.
The insight required to decide whether or not a particular set of
formulae can or can not be used to solve a given problem is difficult
to replicate in a program. Expansions must be checked and programmed
with extreme care, since the influence of errors in higher terms can
be easily mistaken for unavoidable numerical noise in the system.
While the assumption of moderate and constant elliptical eccentricity
might be valid for terrestrial problems, it represents an undue
limitation in systems incorporating orbital geometry. Finally, in
most computer hardware environments the full number of significant
digits required to achieve sub-millimeter resolution can be used
without any penalty in the execution time.
With the appropriate statement of conditions, all ellipsoid geometry
problems of single periodic nature (i.e. those whose differential
geometry statement does not lead to elliptic integrals) can be solved
very efficiently, to any desired level of precision, using an
iteration technique based on the alternate evaluation of conditions
near the surface and at the point where the normal is closest to the
coordinate origin. Ellipsoid coordinates consisting of three
direction cosines offer significant advantages in all numerical
algorithms required to carry out this iteration. The distinct
advantage of this method (compared to a program based on expansion
formulae) lies in its automatic self-adjustment to the computational
load. The number of iterations will depend on the precision
criterion, physical size of the problem and the measure of ellipsoid
(or ellipse!) eccentricity. The same program can therefore be used
for all global geometry problems of a given type, with full confidence
that the desired precision has been achieved - in each individual
invocation - through a minimum number of arithmetical operations
necessary.
This approach can be applied not only to conventional geodetic
problems but also to solve problems dealing with both surface and
spatial entities. In particular, it will be effective solving the
problems which deal simultaneously with the ellipsoid surface and with
orbital parameters which are themselves of quadric nature.
It should be noted that only the framework data must be permanently
retained in global ellipsoid coordinate values. As explained below,
volume data coordinates can be stored in a much more efficient format,
and transformed into ellipsoid coordinates in transient mode, whenever
these are required.
Surface Partitioning And Location Indexing
One of the essential facilities required for the design and
construction of a geographical database is a surface partitioning
scheme. On the simplest level, this provides a basis for indexing and
retrieval of location-specific data. Even more important will be its
use for efficient run-time evaluation of spatial unions and
intersections, probably the most critical facility in construction of
a fully relational spatial database system.
Where the potential for extended coverage is required, the
partitioning scheme must be capable of dealing with the complete
ellipsoidal surface. This can not be achieved using any of the
regular tessellations which have been proposed as the base for
hierarchical data-cells: beyond the equivalent of the five Platonic
solids, the sphere can not be divided into a finite number of equal,
regular surface elements.
Various schemes based on latitude/longitude "rectangles" are often
used for large coverage or global databases. However, resulting cell
network is hard to modify in size and density, high-latitude coverage
can be restricted or inefficient, and in most cases the approach
forces the use of unwieldy angular coordinates.
By contrast, the partitioning scheme used in the Hipparchus model
is based on spheroidal cells analogous to planar Voronoi polygons.
The definition of the structure is simple. Given a set of distinct
(center)points, a spheroidal polygon-cell corresponding to one of them
is defined as a set of all surface points "closer" to it than to any
other member of the centerpoint set. For each surface point, the
minimum "distance" to any point in the set of centers can be
determined: if there is only one centerpoint at such a distance, the
point is within a cell. If there are two, it belongs to an edge. If
there are three, the point is a vertex. A dual of the set of polygons
is obtained by connecting the centerpoints which share an edge.
The application can define a pattern of cells by any purposefully
distributed set of centerpoints. Since these are defined by their
normals, the partitioning scheme is completely free from condescending
to any numerically singular surface point. The distribution of
centerpoints can be based on any combination of criteria selected by
the application: data volume distribution, system activity patterns,
maximum or minimum cell size limits. It can even represent an existing
set of spatial framework items, e.g. geodetic control stations.
A sort-like algorithm produces the digital model of the dual. The
cell frame structure is thus reduced to a list of global, ellipsoid
coordinates of centerpoints and a circular list of neighbor
identifiers for each cell. If the application requires that a limit
be placed on the maximum "distance" between neighboring centerpoints,
the algorithm must be capable of bridging the "voids", and null items
must be recognizable in the circular list. This data structure is
used extensively by all spatial algorithms. Unlike systems in which
location of the cell is implied in its identifier, the Hipparchus
model requires explicit recording of the global coordinates of cell
centers. Method of storage and access to this data can therefore have
considerable influence on the efficiency of spatial processing.
A cell is assigned an internal coordinate system with the origin at
its centerpoint. As mentioned before, the mapping function between
global and cell systems is an ellipsoid-modified stereographic
projection. The "transformation algorithms" (in both directions)
consist therefore of nothing but a few floating-point multiplications.
"Finite Element Cartography". If a large volume of data has to be
transformed into output device coordinates based on a specific
conventional cartographic projection, only a few points on the cell
(or the display surface) frame will have to be transformed using a
rigorous cartographic projection calculation. Based on the frame
data/display correspondence, parameters of a simple polynomial
transformation are easily calculated. Volume transformations will
again require only a few multiplications, and can be set to produce
the result directly in hardware coordinates of an output device. This
type of manipulation can be of particular value if a complex
geometronical function has to be applied over the complete surface of
a dense data set, for instance in transient cartographic restitution
of digital remote sensor image material.
One of the most often executed algorithms in the model will probably
be the search for the "home cell" of an arbitrary global location.
Selection of the first candidate cell is left to the application, in
order to exploit any systematic bias in either transient or permanent
location reference distribution. A list of all neighbors is
traversed, and distances from the given location to the neighbor
centerpoints are determined. If all these distances are greater than
the distance from the current candidate centerpoint, the problem is
solved. Otherwise, the minimum value indicates a better candidate.
While the algorithm is very straightforward, its efficiency will be
extremely sensitive to the selection of the spheroid "distance"
definition and numerical characteristics of global coordinates. The
same will apply to most combined list-processing and numerical
algorithms employed by the model.
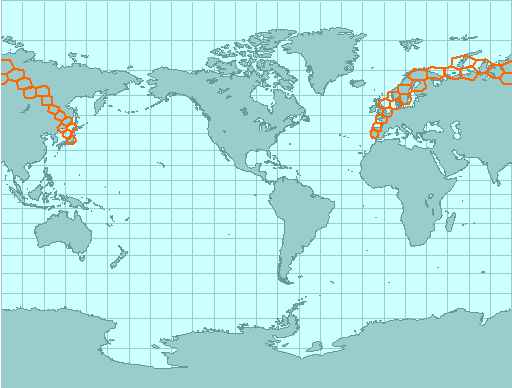 Fig. 2: Trace of home cell search algorithm
Fig. 2: Trace of home cell search algorithm
While Voronoi polygons have often been used in computer algorithms
solving various classes of planar navigation problems, at the time of
this writing no record was found of the use of an equivalent global,
spheroidal structure as a partitioning scheme in a geometronical
computer system.
Modelling Of Spatial Data Objects
Points: Digital representation of a point data element is simple:
it consists of a cell identifier and local (cell) coordinates. Even with
fairly large cells, the global-to-local scaling will ensure equivalent
spatial resolution in case where local coordinate values have only
one-half of the significant digits used for global coordinate values.
Since the efficiency of external storage use and the associated speed
of I/O transfer can be of extreme importance in a large database, the
following numerical data are of interest:
If a 64-bit global, a 32-bit local coordinate values and 16-bit cell
identifier are used, the volume data point representation will require
only 80 bits, and will still yield sub-millimeter resolution.
80 binary digits are capable of storing 2**80 (approximately 1.2E24)
distinct values; the surface of the Earth is approximately 5.1E20
square millimeters. The ratio of these two numbers (approximately 69
out of 80) represents the theoretical memory utilization factor;
practically, the margin allows significant variation in cell size and
use of various computational conveniences (floating point notation,
cell range encoding, e.t.c.). This utilization factor compares to 69
bits out of 128 if the point is represented by latitude/longitude in
radian measure, and 69 out of 144 bits (typically) if a conventional,
wide-coverage cartographic projection system plane identifier and
coordinates are used. Furthermore, various external storage
compression schemes that take advantage of the re-occurring cell
identifier are likely to be significantly simpler and more effective
than any compression scheme of a pure numerical coordinate value.
It is important to note that in Hipparchus model cell coordinates
of a point are not used for a numerical solution of metric problems; their
purpose is to provide a compressed coordinate storage format for
high-volume data, and to facilitate generation of the transient,
analog view of the data.
Lines: One-dimensional objects are represented by an ordered
list of cells traversed by the line, and - within each cell - a list,
(possibly null) of vertices in the point format described above. If
the application requires frequent evaluations of spatial unions and
intersections, it might be efficient to find and store permanently all
points where lines cross cell boundaries. Their internal
representation (permanent or transient) is somewhat modified in order
to restrict their domain to the one-dimensional edge, but their
resolution and storage requirements will be comparable to the general
point format used by the model.
Regions: Two-dimensional objects are represented by a directed
circular boundary line and an encoded aggregate list of cells that are
completely within the region. When compared to simple boundary line
circular vertex list, this structure makes the evaluation of spatial
relationships significantly more efficient. The solution will often
be reached by simple manipulation of cell identifier lists, instead of
the evaluation of boundary geometry. The number of cases where,
ceteris paribus, this will be possible, will be inversely proportional
to the average cell size. (In example in Fig. 3, boundary geometry
examination will be confined to three cells.) This representation of
a two-dimensional object is a combination of the traditional boundary
representation and schemes based on regular planar tessellations. It
offers the high resolution and precision usually associated with the
former, while approaching the efficiency of relational evaluations of
the latter. In addition, it does not violate the true spherical nature
of the data domain. For instance, if [A] is a region, then NOT [A] is
an infinite, numerically ill-defined region in a plane. By contrast,
on any spheroidal surface NOT [A] is the simple finite complement.
 Fig. 3: Intersection of two-dimensional objects
Fig. 3: Intersection of two-dimensional objects
Orbit Dynamics: Practice abounds with examples of problems
encountered in attempts to integrate remote sensing and existing terrestrial
data. Even in instances where the spatial geometry can be defined with
sufficient precision, it is common to cast (by "pre-processing") the
digital image produced by a satellite sensor into a specific plane
projection system and pixel aspect ratio and orientation. This
unnecessarily increases the entropy of remotely sensed data available
to applications requiring different or no planar castings. In many
instances, problems will disappear if the application is given the
ability to manipulate the original, undistorted, observation geometry.
A general-purpose geopositioning software tool must therefore provide
efficient evaluation of basic time/geometry relationships within the
orbital plane, and the ability to transfer the locations from an
instantaneous orbit plane to its primary frame of spatial reference.
(More complex calculations are probably application-specific and are
restricted to infrequent adjustments of orbit parameters.)
The geometry functions described already suffice to define any orbit
at the convenient epoch - e.g. the time of the last parameter
adjustment. To find a position (in the orbital plane) of a platform
at a given time, a direct solution of the problem postulated by
Kepler's second law is required. (Same as in geodetic problems
mentioned previously, this "direct" problem requires an iteration,
while the "inverse" yields a closed solution.) Any increase of orbit
eccentricity will affect the number of iterations, but the same
software component can be used to solve both near-circular and steep
orbits. Common 64-bit floating point representation will preserve
millimetric resolution even for geosynchronous orbits. Rigorous
modelling of general precession can be achieved simply by an
additional vector rotation about the polar axis. This is combined
easily with sidereal rotation, required in any case for transfer of
position between the inertial and terrestrial frames of reference.
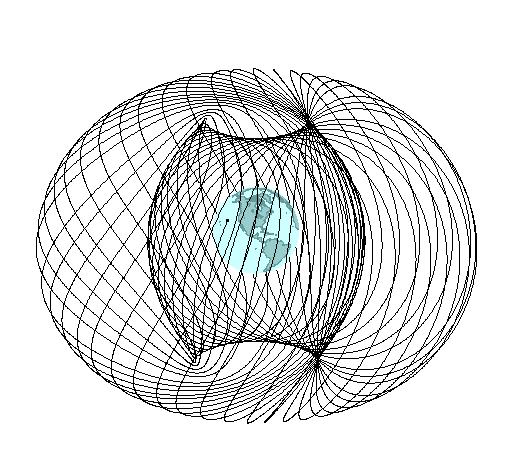
Fig. 4: Orthographic view of a precessing orbit
Conclusion
Use of computers in mapping is as old as the computer itself: the
first commercially marketed computer, UNIVAC 1, was used in 1952 to
calculate Gauss-Krueger projection tables. With the development of
computer graphics, it quickly became common to store and update a
graphical scheme representing a map. Until very recently, the main
object of this process remained the production of graphical output
that was not substantially different from a conventional analog map.
While the production of the map was thus computerized, the ability of
an "end-use" quantitative discipline to employ a computer to solve
complex spatial problems was not addressed. The use of a "computer
map" was precisely the same as that of a traditional, manually
produced document.
All quantitative disciplines are facing the same demands as
cartography to increase precision, volume and complexity of data which
can be efficiently processed. Hence, computer applications in those
disciplines require "maps" from which spatial inferences can be
derived not only by the traditional map user, but also by a set of
computer application programs. To a limited extent only, this has
been achieved in applications which could tolerate severe limitations
on area of coverage, data volumes, or spatial resolution requirements.
Location attributes in these computer systems are usually based on an
extended coverage ellipsoid-to-plane conformal projection: a numerical
model developed for a completely different purpose.
Computer systems requiring extensive spatial modelling combined with
high resolution and global coverage need powerful yet efficient
numerical georeferencing models. It is unlikely that these can be
based on conventional cartographic techniques. Numerical methodologies
designed specifically for the computerized handling of spatial data
have the best potential for providing generalized solutions.
...
|