Point Nemo is defined as that point on the world's oceans that is furthest away from any land.
Determining the geographic coordinates of such point is also known as the “longest swim” problem. But the solution to that problem requires not only the coordinates of Point Nemo, in addition it requires the knowledge of the length of the swim, and precise identification of point or points on the coast that are closest to it.
Barring some singularity cases which do not occur on the coastline of physical Earth, that point will be at equal distance from exactly three points on the coastline.
It is quite easy to explain why:
Any point which we might consider to be Point Nemo, that has only one closest point on the coastline, could be moved by an infinitesimally small distance in the direction away from the closest coast point, which means it can't be the point as defined in the preamble.
After a number of such small shifts of its position, the point would reach a location where it is at exactly the same distance away from the original near point, and some other point on the coast.
Even then, the point will not be the one we are looking for.
The point could again move, this time away from two points, in the direction opposite from the mid-direction to them, but so that it remains equally distant from both of them.
If this conceptual process of infinitesimally small shifts results in the point location which is equally distant from three points on the coast, and if there is no other point with a closest point on the coast more distant than one we considered, the problem of the longest swim is solved.
In addition to determining the coordinates of Point Nemo, we must also determine the coordinates of three "proximity vertices" on the coastline, because without knowing what they are, as well as what is the distance from Point Nemo to them, we can not confirm that our solution is correct. Specifically, if among all the points on the coast we can find one or more that is closer than three "proximity vertices", the solution is clearly incorrect.
If we want to engage in computational geometry as used by contemporary surveying and mapping, the Earth must be considered an ellipsoid of rotation (often called simply "spheroid"). The point position is numerically represented by φ and λ, ellipsoid latitude and longitude. The latitude is the angle between the point's ellipsoid normal and the equatorial plane, and the longitude is the angle, measured in the equatorial plane, between the projection of the normal and the projection of some agreed-upon prime meridian. The distance between any two points on the ellipsoid is the length of geodesic (i.e., the shortest line connecting two points that lies completely on the surface of the body they are located on).
Simplifying the geometry calculations by considering the points to be on the surface of a sphere, and the distance between them to be the length of a great circle segment might be adequate for some practical applications, but this does not represent the geometry of our planet adequately in any activity requiring precise measurements over even moderately large areas - let alone when whole continents or oceans are involved.
Using the only world coastline data set publicly available in 2002 (DCW, with 1.3 million coastline vertices), I used the longest swim problem to demonstrate the efficiency of spatial sort and search capabilities provided by a software product named the Hipparchus Library. The principles of it were first published in 1987 at Auto-Carto 8 in a paper that can today be seen at www.lukatela.com/hrvoje/papers/hlauto8.html . It organized point, line and area objects by clustering their vertices in a spheroidal Voronoi cell grid, as depicted here:

With that, it was determined that Point Nemo coordinates - and, as it turns out much more significantly, the coordinates of three equidistant minimum proximity vertices, located on three Pacific islands - are:
Coordinates of Point Nemo: -48.8754854 -123.3925193 and Nemo Proximity Vertices: -27.2081400 -109.4592000 motunui -72.9658400 -126.3752202 maher -24.6776000 -124.7905200 pandora and the equal distance of Point Nemo to three vertices: 2688220.580 .
(φ and λ defined as above and measured in decimal degrees, distance in meters, geodetic datum and spheroid WGS84. The calculation was performed with millimetric numerical precision and the results published (in the current form) in 2004) cf.: www.lukatela.com/pointnemo ).
This can be shown on a map:
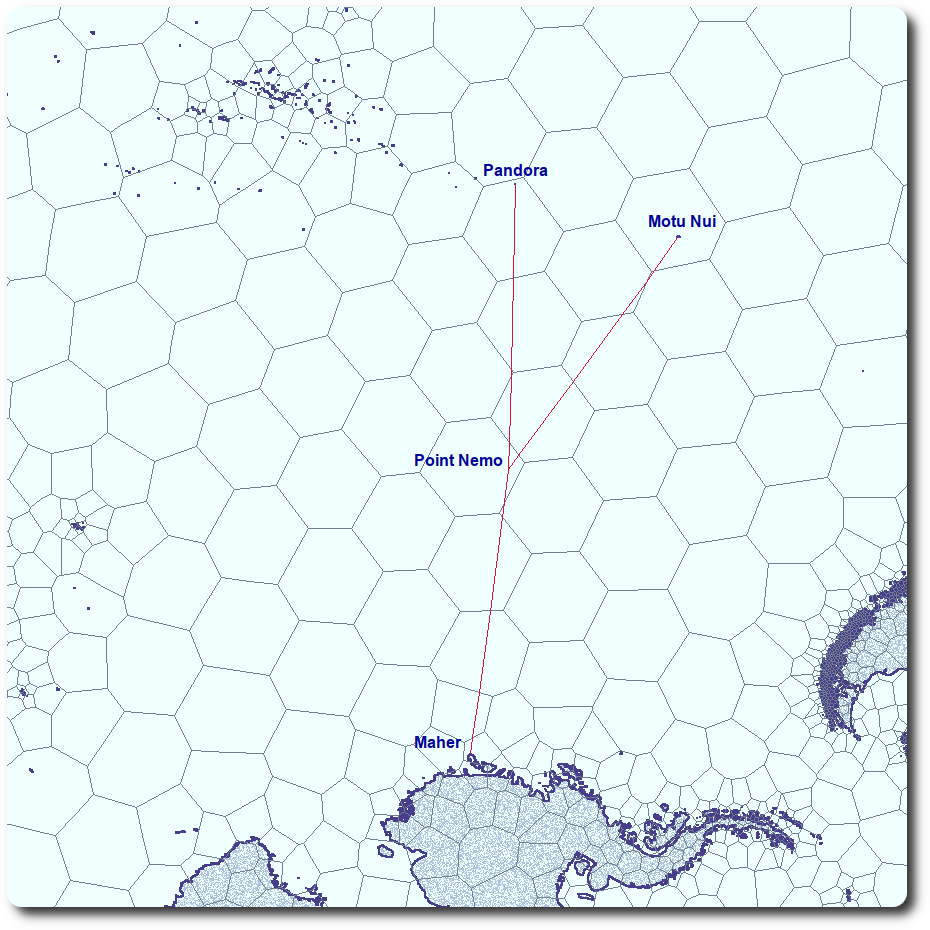
Not surprisingly, all three Nemo Proximity Vertices are islets just off the coast of three somewhat larger Pacific islands:
Motu Nui is the largest of three small islands, southwest of the well-known and much larger Rapa Nui (Easter Island), today part of Chile. The proximity vertex is the southernmost tip of Motu Nui. (cf.: https://en.wikipedia.org/wiki/Motu_Nui)
Pandora is not more than a sandy bar, one of the islets that form the southern rim of uninhibited Ducie atoll. Ducie is part of Pitcairn island group, today part of the British Overseas Territory in the Pacific. The proximity vertex is the southernmost part of its outer sandy beach. (cf.: https://en.wikipedia.org/wiki/Ducie_Island)
Maher is a small, rocky island approximately 10 km north of Siple Island, which is permanently connected to the continent of Antarctica by Getz Ice Shelf. Maher is reported to be occasionally free of sea-ice cover during the short Antarctic summers. The proximity vertex is the northernmost tip of the island. (cf.: https://en.wikipedia.org/wiki/Maher_Island)
Other world coastline data sets appeared since that time.
One of the most commonly used today is Open Street Map (OSM) coastline data file, "coastlines‑split‑4326.zip" available from OSM download server; from which the shape file coastline representation can be extracted, and which can in turn can be transformed into a .csv file of approximately 70 million vertices.
Using the same software as that used for DCW computation in 2002, the results are:
Coordinates of Point Nemo: -49.0025795 -123.3918598 and three Nemo proximity vertices: -27.2022152 -109.4535548 motunui -73.1904913 -127.0394760 maher -24.6889471 -124.7868066 pandora distance to proximity vertices: 2701065.833
It is important to note that the Nemo Proximity Vertices are the very same three locales on the world's coastline as they were in DCW computational results published in 2004, but their coordinates shifted (in meters), as follows:
Pandora: 1311.893 Maher: 33084.802 Motu Nui: 862.445
Maps of the local area of three proximity vertices are the best way to present the above numbers. They depict the landmass and coast line constructed from both DCW (somewhat coarse) and OSM (somewhat higher density) datasets, and the line from each proximity vertex towards the distant Point Nemo. While it is often tacitly assumed that higher density/resolution geographical data will also be of higher spatial precision, there is no guarantee at all that this is the case here. If anything (see below in this text!) we have good reasons to question this assumption).
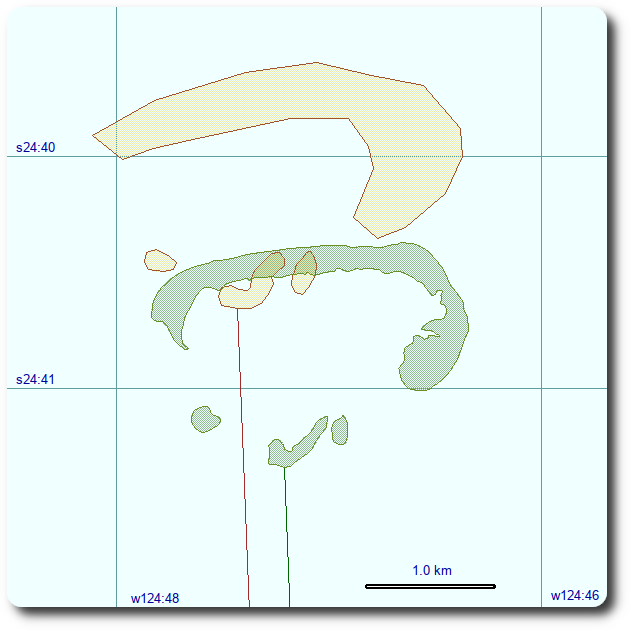
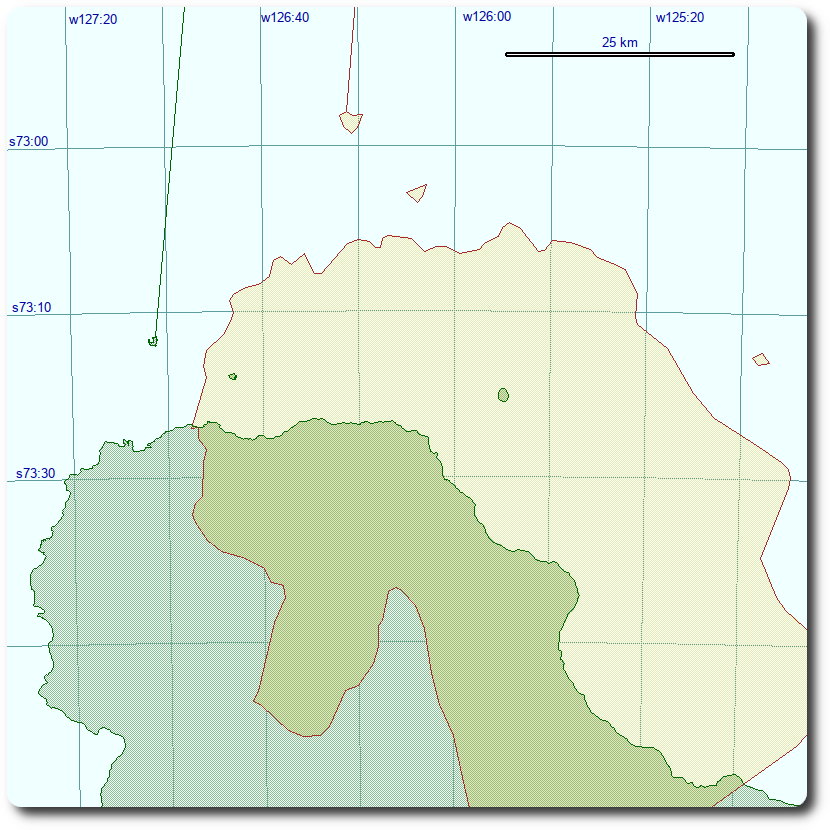
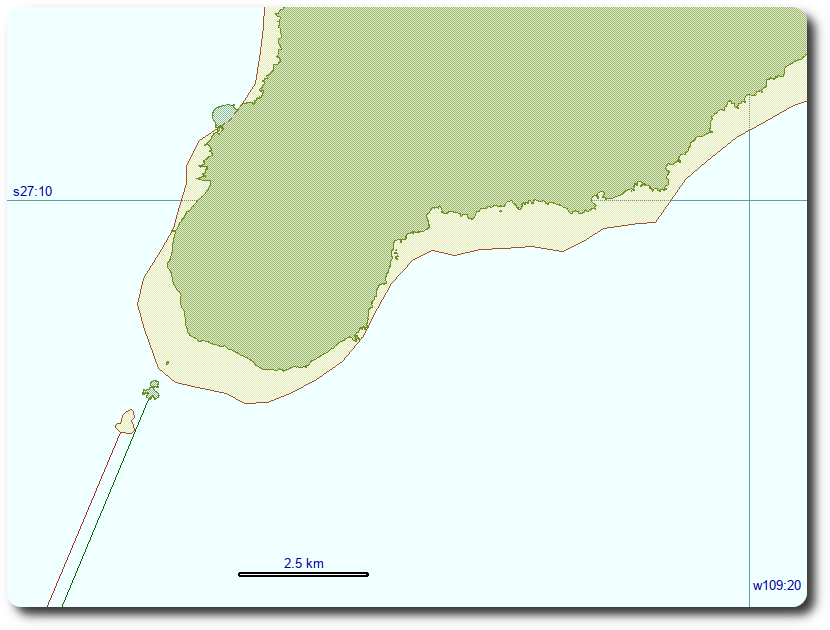
The location of two mid-pacific islands changed by approximately a kilometer in each case. On the other hand, the location of the proximity vertex near the coast of Antarctica differs by more than 30 kilometers. A reasonable explanation for this is the likely absence of any ground survey of the coast of Antarctica, the difficulty in determining where exactly is the boundary between sea and land when it is hidden under the sea-ice and, last but not least, inadequate geodetic datum transformation in the process of merging data from different sources. It is quite telling that the major land-mass south of the minuscule Maher - rather large Siple island - is shown as an island by DCW, and as an integral part of Antarctica by OSM coastline.
The difference in Point Nemo coordinates determination between 2002 (from DCW coastline) and 2022 (OSM coastline) are clearly attributable to the changed coordinates of three proximity vertices, most notably the one near the coast of Antarctica.
If we test the OSM calculated Point Nemo coordinates using a very simple program that calculates the length of geodesic between Point Nemo and every vertex in the OSM coastline file, and list only those that are within claimed proximity (plus a millimeter or so of "computational fuzz"), it would return three (and ONLY three), vertices, as follows:
-27.2022152 -109.4535548 94347 -24.6889471 -124.7868066 272788 -73.1904913 -127.0394760 355869
Those are indeed the extremities of three different small Pacific islands. (The third value in the row is OSM shape file line segment identifier - this makes vertices easy to identify in the 70 million lines large .csv file).
Such traverse of the coastline data file is a necessary conclusion of any method that searches for the coordinates of Point Nemo; it confirms the results, regardless of the method used to perform the search for proximity vertices in a computationally feasible number of computer instructions.
To my knowledge, no other landmass (i.e., some small - perhaps minuscule - South Pacific island) emerged in any coastline file published so far that would be located so that that it would produce a different set of proximity vertices than those determined by both DCW source data, and the computation presented here using OSM coastline data.
Those that are more interested in physical Earth than in spatial sorting and searching and geodetic computations have an interesting alternative. Instead of searching for the coordinates of Nemo proximity vertices in various published geographical data collections (DCW, OSM, etc.), one can find out what their location is by some other, more "direct" method.
The simplest among those might be to consult public on-line map and satellite imagery servers.
For instance, if one points the browser with Google maps/earth to the location of three Pacific islands on which (now almost certainly!) Nemo proximity vertices are located, possibly alternating between "map" and "satellite" view, the partial content of the browser window will probably look something like this:

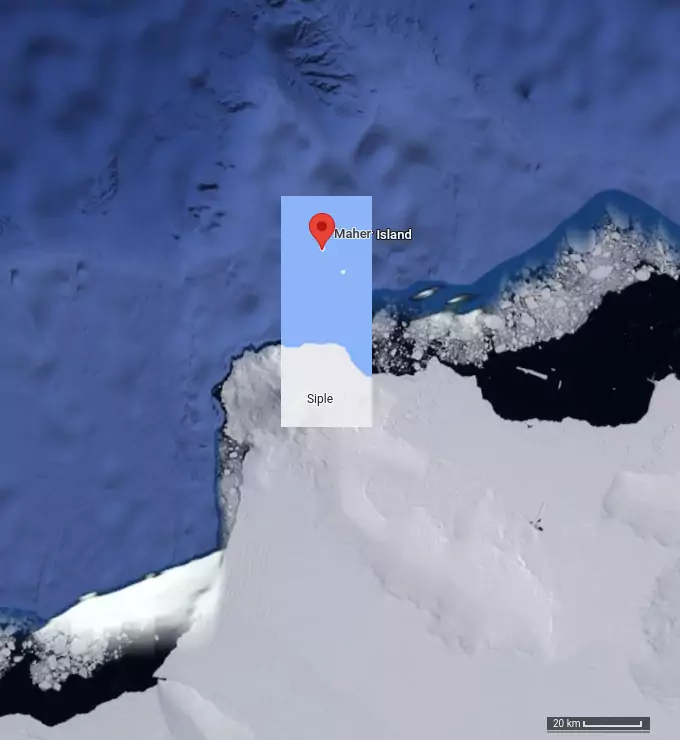

"Right-clicking" the points on the northern (Maher), south-eastern (Motu Nui) and southern (Pandora) island extremities will produce:
Pandora -24.688826 -124.786763 Maher -72.965768 -126.375714 Motu Nui -27.202332 -109.453776
(Numbers given above are still of an order of magnitude higher numerical resolution than that which can ever be obtained by identifying a pixel on a rather low resolution image).
No clever spatial sorting and searching is then required: the only computational device needed is a function performing the computation of the length of geodesic and a triangular iterative algorithm that will converge when three distances are the same - perhaps 100 lines of code in all. With this, and as a confirmation of soundness of Point Nemo determination using any present and future published coastline data file, we get:
Point Nemo coordinates: -48.88120089 -123.34616041 (or -48°52'52",-123°20'46" as angular φ and λ) with the proximity of 2687784 meters.
It is quite interesting to see the map in the Point Nemo vicinity, with all three versions of its coordinates discussed in this text:

Nemo Library is a small software suite that can provides those with a certain minimum of programming skills the ability to quickly reach the point where thay can perform most or all Point Nemo processing and verification described in the paragraphs above.
An even better approach might be to actually visit both Motu Nui (Rapa Nui) and Pandora (Ducie) and leave a GPS device on the identified proximity point to sample the location over a period of several hours. Such a project is well within the means of an individual.
On the other hand, exploring the ice-shelf conditions on Maher (northern reaches of Siple Island), visiting the location and determining the northernmost point of land likely hidden under the ice would probably require an organized effort by a large governmental agency. It would, however, be worth while, as it would turn the search for Point Nemo from a never-ending series of exercises in spatial sorting and searching and geodetic computations, using third-party data which lacks any spatial precision attestation, into a discussion of the world-wide precision of the current generation of three principal satellite positioning systems - not in millimeter, but probably well in the range of tens of meters.
An even better solution will come about in a rather distant future, when we will finally have the technology capable of measuring the distance between two points that are well below the horizon to each other directly, instead of using an auxiliary station on a fast-moving platform, undulating in a statistically modeled near-space orbit, subject to the uneven distribution of the planetary masses. Then, and only then, will we know the millimetric position of Point Nemo - not as an artificial product of our superior computational abilities, but as an exact physical measurement.
Until that day, all we can say with any certainty is that Point Nemo is located somewhere in the South Pacific, at equal distance from Pandora, Maher and Motu Nui - just as that 2002 DCW coastline based computation (published in 2004) indicated.
Hrvoje Lukatela, September 2022
Contact: www.lukatela.com/hrvoje