NON-ISOTROPIC GEOGRAPHIC MODELING
Waldo Tobler
Five of the most important and useful theoretical models in the study of geography are, in historical order: the
Von Thunen model of agricultural land use; Weber's model of industrial location; Walter Christaller's central place
formulation; the gravity model of spatial interaction; and Hagerstrand's model of the geographical spread of innovation.
All of these models are of fundamental importance in understanding the world around us. They also have in common
the fact that they simplify reality by invoking an isotropic geographic space. Of course they do this to varying degree,
and some then relax this assumption. Most of them are also computationally explicit models,
again to varying degrees. Both of these aspects of the models are the subject of my discussion.
Current Geographic Information Systems have the potential of overcoming the isotropic plane assumption,
even though the elegant pedagogic simplicity of models using this assumption will always obtain. Consider first the
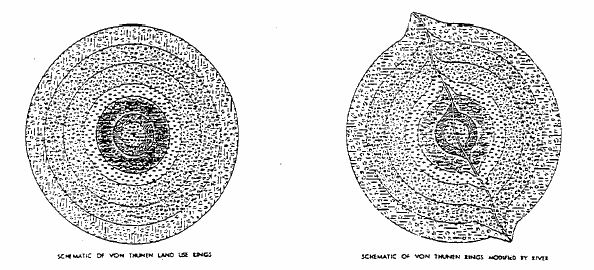
Von Thunen model. Here agricultural land use patterns are derived as a function of market price, transport cost to
market, and agricultural production costs. Under the isotropic assumption, and a single market, the geographic
arrangment of crops and land uses takes the concentric form. Years ago, for an Economic Geography class near Detroit,
I wrote a simple computer program to demonstrate this, with five commodities, including strawberries, wheat, other
foodstuffs, and Cadillacs. Given the other inputs I could demonstrate computer printouts of circularly arranged optimal
land uses, and could even run the program with multiple market places to get mixtures of partially concentric patterns,
and could include a climatic gradient to get non-circular patterns. All this was done off-line, in a batch environment
(circa 1965). My computer program could not incorporate positional variations in transportation cost, even though Von
Thunen himself gave such a demonstration introducing a river into the geographic space (Figure I).
Several GISs can now provide more realistic calculations. One of our graduate students, R. Dodson, has
implemented the Von Thunen model within the IDRISI system, and has done some work on an implementation of the
Weber model. This system allows variable transportation costs to be included. However he still uses synthetic
landscapes. But this need not be the case. To see how this can be improved upon, I would like to contrast the situation
with a popular computer pastime. What I have in mind is the "Flight Simulator" in which one can pretend to be an
airplane pilot. The geographically interesting part is that one can purchase a variety of landscapes, and "fly" around
these. Each of these "landscapes" or airport vicinities, can be purchased separately. Imagine having the same thing for
the USA, or the world, and running Von Thunen, Weber, Christaller, or Hagerstand models on real landscapes. For, say
$20, you might purchase "The Los Angeles Region" as a backdrop for your "spread of AIDS" model, or whatever
model excites you. I envision the day when we can purchase alternate geographic landscapes for such geographical
simulations. These would contain real geographic data (soils, transportation, population, etc., depending on
the class of model), for a particular place, region, nation, or continent (or even time period). Indeed, I propose that
we consider the development of such a library of modules. The trend is clearly in this direction, and a
few prototypes already exist, the Digital Elevation Models and Digital Line Graphs of the US Geological Survey,
and the TIGER files of the US Bureau of the Census being two primitive (but useful) examples of proto-modules.
A common element in many geographic models is the assumption of Euclidean distance; this is generally the
basic postulate of the isotropic plane. How can a model such as that of Christaller relating central places be adapted to
fit the highlands of some country in a pre-automobile time? Can it be modified to take into account todays of complex
transportation systems which distort topological and metrical realtions? Current Geographic Information Systems
indeed enable one, given a transportation disutility on a particular class of land, to calculate more realistic
time- or cost-distances between places. I find this particularly exciting
and have worked out a simple example for walking in variable terrain using the hiking function (Figure II)
estimated from empirical data given by Imhof (1950, pp 217-220).

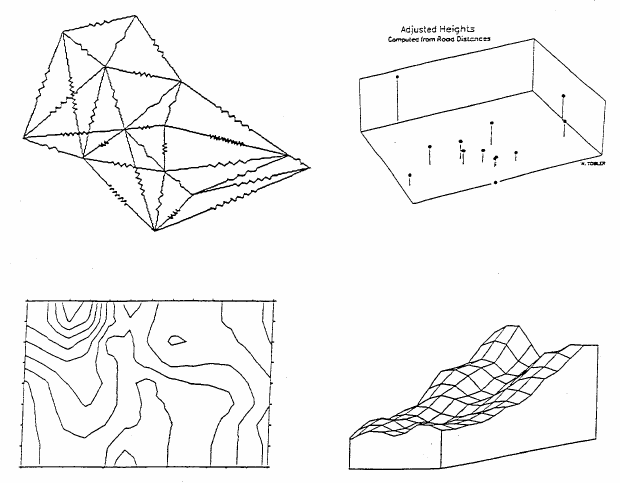
In order to use this function one simply calculates the slope of the terrain, and then converts this to a walking
velocity. It is easiest to do if the terrain is given in the form of a geographic "matrix", with elevations at equally spaced
increments in two directions (Figure III).

Then one can compute, from any inital point, the minimum time path to all other places (Figure IVa).
Connecting places at equal time-distances yields isochronic lines, or "geographic circles" (Figure IVb). Putting in the
gradients to this contour map then yields two sets of orthogonal lines (Figure IVc), isomorphic with

Gauss' geodesic polar coordinates for which the metric takes on a particularly simple form. Now it would
make sense to reformulate Christaller's central place model in terms of a general Gaussian metric (of the form
 ).
Unfortunately transportation facilities with modern railroads, highways, and airplanes
introduce topological complexities which are not easily treated within the framework of continuous Gaussian
manifolds. This is because real geographic circles have holes and disjoint pieces (Figure V; Tobler 1961). Geographic
Information Systems with these capabilities generally are forced to use network models.
).
Unfortunately transportation facilities with modern railroads, highways, and airplanes
introduce topological complexities which are not easily treated within the framework of continuous Gaussian
manifolds. This is because real geographic circles have holes and disjoint pieces (Figure V; Tobler 1961). Geographic
Information Systems with these capabilities generally are forced to use network models.
The computablity of the theoretical models also raises a pedagogic issue. Current Geographic Information
Systems seem to appear in three contexts. One use is in applied fields; the bureaucratic inventorying of natural
resources or facilities management. A second use is in research, where specific problems are under investigation. Here
attempts are now being made to incorporate various sorts of additional spatial analysis capabilities into GIS's. The third
appearance of GIS's is in courses on GIS. What is missing is their appearance in substantive geography courses such as
Historical Geography, Political Geography, Economic Geography, Cultural Geography, Physical Geography, Regional
Geography of Country X or area Y. Now imagine some future date when all of these courses are lab courses, or have a
laboratory associated with them, as most physical geography courses (and some others) already have. As I see it this
lab might be a computational GIS lab. The point is to bring the GIS into the substantive courses (not only in
geography), and not to leave it in an isolated GIS techniques course. I recently taught a course on human migration and
made one of the hours into a set of computational exercises. Professor Golledge has been using SimCity in a similar
manner in his course on Urban Geography. Going somewhat further, imagine that all social science courses might
come with a computer lab some day in the future. Not just for word processing, but real Computational Social Science.
There is a clear tendency in that direction which needs to be encouraged.
REFERENCES
-
Christaller,W (1935):
Die zentralen Orte in Sueddeutschland,
J. Fischer, Jena.
-
Dodson,R (1991):
VT/GIS The Von Thunen GIS Package,
Technical Paper 91-27, Santa Barbara, NCGIA.
-
Dussart,F (1959):
"Les courbes isochrones de la ville de Liege pour 1958-1959",
Bull. Soc. Belge d'Etudes Geogr. XXVIII, 1:59-68.
-
Hagerstrand,T (1968):
"A Monte Carlo Approach to Diffusion",
pp 368-384 of Berry, B; Marble, D: Spatial Analysis, Prentice Hall, Englewood Cliffs.
-
Imhof,E (1950):
Gelaende und Karte,
Rentsch, Zurich.
-
Riedel,J (1911):
"Neue Studien ueber Isochronenkarten",
Pet. Geogr. Mitt., LVII,1:281-284.
-
Tobler, W (1961):
Map Transformations of Geographic Space,
PhD dissertation, Seattle, University of Washington
-
Von Thunen,J (1826):
Der Isolierte Staat in Beziehung auf Landwirschaft und Nationaloekonomie,
G. Fischer, Jena; 678 pp.
-
Weber,A (1909):
Ueber den Standort der Industrien,
Tuebingen.
Presented at the NCGIA sponsored conference on Geographic Information Systems in the Social Sciences,
Santa Barbara, Feb. 1991
SPECULATIONS ON THE GEOMETRY OF GEOGRAPHY
Waldo Tobler
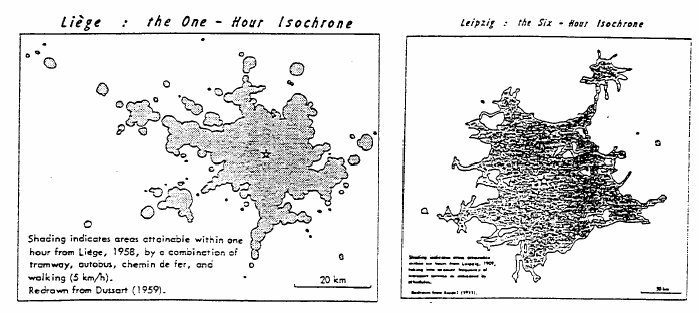
Consider the set of all places on the surface of the earth which you could reach within one hour of where you
are now. The outer edge of this set forms a geographical 'circle' of one hour radius. Francis Galton introduced the term
isochrone for such a circle in the 1880's, but the word (in a somewhat different context) was probably already used by
Snellius or Bernoulli.
What a curious circle it is! Its circumference is hardly 2*pi*r, its area, in square hours, is not pi*r^2. The circle
most probably has holes in it, and probably consists of disjoint pieces when shown on an ordinary geographical map.
The shape of this circle depends on the place and time of day at which you start your journey. Our daily environment,
as a geometry, seems more complicated than the Riemannian geometry envisaged by Einstein, at least as far as map
images on the earth are concerned. A resident of Paris will have a geographical circle of one hour radius with a
different circumference, shape, and area from that of a person in Los Angeles. This is a bit like the geometry on the
surface of a cucumber; here a circle at the narrow end will differ from one near the middle. A familiarity with non
Euclidean geometry renders this quite understandable. Next, try drawing concentric circles on a potato from some
starting point. Now put in the orthogonal trajectories to these circles. Then note the similarity to Gaussian polar
geodesic coordinates. This is usually obscured because the radial geodesics are usually not drawn on geographical
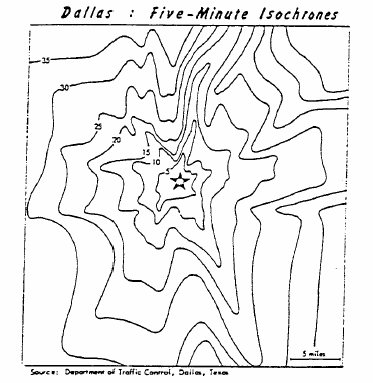
isochronic maps. The map of travel times from central Dallas is typical.
The analogy to non Euclidean spaces clearly suggests that one try to model at least a part of our travel time
geometry as a two manifold of variable curvature.
To this end I have assembled several tables, of which the following
is a short selection:
- Road distances between cities in Switzerland.
- Automobile travel times between these places.
- Similar data for Austria.
- Travel times between addresses in New York City.
- Airline travel times between cities in the United States.
- Airline travel costs, in dollars, amongst the foregoing.
- Bus travel times and costs between the above cities.
- Parcel shipment costs between cities in the U.S.
- Distances between US cities estimated by a sample of individuals.
- Ocean route lengths between world ports.
In each instance the location names (i.e., latitude and longitude) of the places are available.
I would now like to model these relationships with an equation of the form (summation convention):

from which the Gaussian curvature, geodesic curvature, etc., might be calculated. A difficulty is that this
metric tensor is derived assuming that Euclidean geometry holds in the small, that is, for very short distances. In
geographic space this assumption is often not satisfied, as noted again below.
A cartographic application might be that one could make polar geodesic maps centered on any place. More
practical usefulness would be obtained if one could directly compute the travel costs (times) between places knowing
only their latitude and longitude, the mode of transportation, and the time of day. This would be like the computation of
spheroidal distances from geodetic coordinates - the sort of thing one does on a hand calculator nowadays. This would
require the storage of the
 coefficients. If these coefficients could not be approximated by simple formulae, which
is likely, then it might be just as easy to do a lookup in a large transport cost (time) table, in effect storing something
like the Official Airline Guide in a small computer. This is probably what will happen, and road maps stored in hand
calculators are not far off.
coefficients. If these coefficients could not be approximated by simple formulae, which
is likely, then it might be just as easy to do a lookup in a large transport cost (time) table, in effect storing something
like the Official Airline Guide in a small computer. This is probably what will happen, and road maps stored in hand
calculators are not far off.
Still, there are some advantages to the theoretical notion. By calculating the Gaussian curvature the amount of
geographic change induced by a freeway in an environment might be estimated. This could be one way of computing
the impact of the road. If a freeway introduces changes in travel time, and one contemplates showing this change as a
warped map, then Tissot's indicatrix provides a measure of the geometric change. Tissot's work is most generally used
to measure the amount of distortion on geographical map projections, and can be computed for any point of a map. In
this novel application the linear, angular, and areal distorting consequences of a change in a transport system could be
calculated. Formal integration of Tissot's measures (which are local in the sense of calculus) over the entire affected
region gives a measure of the total effect. It is interesting to note that the impacts include angular displacements as well
as the linear and areal ones which one would expect. One also expects these impacts to decline with distance from the
locus of accessibility change. Tissot's indicatrix is related to the strain tensor as used in mechanics and, and to the
metric tensor of differential geometry.
There are some empirical problems introduced by these ideas, namely:
-
The Gaussian metric formula gets lengths by summation of short segments along a geodesic. Thus the
data tables need to be parsed so that they contain only the minimum paths, i.e., the direct connections.
This is not particularly difficult and I have written a computer program for this purpose, making use of the
triangular inequality. The figures show two attempts to represent a small subset from one of the data
tables. In both instances the location of the places is fixed. One method lengthens the direct connecting
lines between the places by introducing wiggles, to obtain an appropriate total length on a flat map. The
second method raises the places into the air so that the slant height introduces a sufficient lengthening of
the distances, in a least squares manner. These methods can be applied no matter what the units are by a
judicious scaling. A travel time topography can thus be created The Gaussian weights might now be
estimated, because we know that the distance stretching is approximated, as a function of direction, by the
ratio

-
Differential geometry needs to be married with the method of least squares to estimate the
 from empirical observations. These observations are irregularly arranged on the surface of the earth, as shown above, and
thus require interpolation procedures to place them at the nodes of a mesh in some coordinate system. Interpolation is
often ackward and always introduces assumptions about the phenomena. These assumptions need careful justification.
A space of constant curvature would simplify things but cannot be assumed.
from empirical observations. These observations are irregularly arranged on the surface of the earth, as shown above, and
thus require interpolation procedures to place them at the nodes of a mesh in some coordinate system. Interpolation is
often ackward and always introduces assumptions about the phenomena. These assumptions need careful justification.
A space of constant curvature would simplify things but cannot be assumed.
-
Empirical observation has already shown that road distances are often simply a linear function of great
circle distances; in Swedish towns one can let
road distance = 1.21 * as the crow flys.
The correlation is very high, not too unexpectedly. In the United States the multiplier is about 1.15 in an eastwest
direction, about 1.21 in the north south direction. The greatest deviations occur in the short distances, near the
origin. Thus the magnitude of the percentage difference decreases with distance. The
 can therefore be expected
to show only minor deviations from their values as computed from the spherical or spheroidal values. Can we then
simply introduce a small "fudge" factor into the formula, but retaining the basic form of the metric tensor? Oceans
complicate this.
can therefore be expected
to show only minor deviations from their values as computed from the spherical or spheroidal values. Can we then
simply introduce a small "fudge" factor into the formula, but retaining the basic form of the metric tensor? Oceans
complicate this.


-
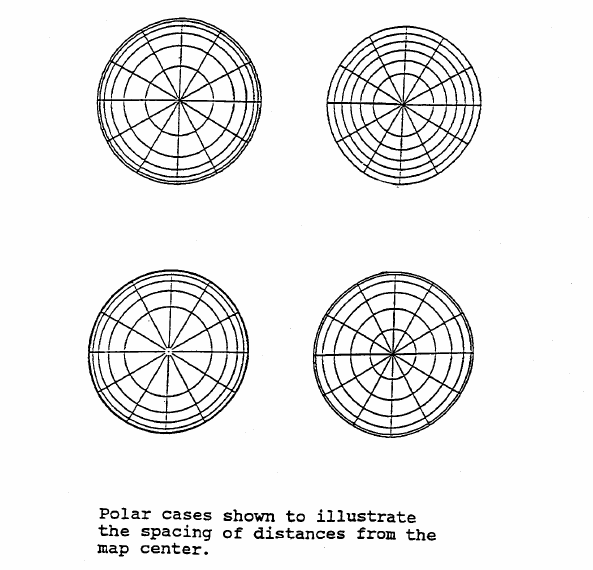
Transport costs usually increase at a decreasing rate with distance, i.e. are concave down. This is easily
translated into an azimuthal map projection,

There are many examples. A short list and illustrations of the earth mapped using these functions are shown.
It is clear that any monotonic (concave down) transportation cost can be approximated by some such function, to
produce maps scaled in cost (or time) from some point. Less obvious is the fact that this can also be done in an area
preserving manner. Lambert's (1772) azimuthal equal area map projection already has this property. Another equal area
map of the globe can be obtained using

This yields a curious map, as shown in the figure. Generally the travel disutilities are different in all directions
so that even more complicated maps need be drawn. But the equations for Gaussian curvature are relatively simple in
polar geodesic coordinates, i.e., knowing that the metric is given by
 then
then
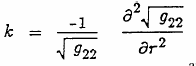
and also

Transportation costs which are non-monotonic with respect to geographic distance, as in the airline cost
examples cited later, render these things more difficult.






-
Many of the tables are not symmetric,
 implying that
implying that
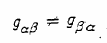 . Will this alone introduce
enough asymmetry into the results? What happens to the rest of conventional differential geometry under these
circumstances? Perhaps one must add a term
. Will this alone introduce
enough asymmetry into the results? What happens to the rest of conventional differential geometry under these
circumstances? Perhaps one must add a term
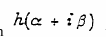 to the equation for ds, as a vector field superimposed on
the distances. I have already calculated an approximate wind field for the United States from a table similar to (e)
above. This is given in the figure. A comparable result should be obtainable from an airline travel schedule, and a
similar notion can be applied to asymmetrical migration tables to compute an implied potential field. This also works
for all sorts of asymmetrical communication or movement tables. Alternately could we use Zaustinsky's model of
"Spaces with Non-Symmetric Distance"? Are Finsler spaces more appropriate? What are reasonable generalizations of
Gauss' work which take these problems into account?
to the equation for ds, as a vector field superimposed on
the distances. I have already calculated an approximate wind field for the United States from a table similar to (e)
above. This is given in the figure. A comparable result should be obtainable from an airline travel schedule, and a
similar notion can be applied to asymmetrical migration tables to compute an implied potential field. This also works
for all sorts of asymmetrical communication or movement tables. Alternately could we use Zaustinsky's model of
"Spaces with Non-Symmetric Distance"? Are Finsler spaces more appropriate? What are reasonable generalizations of
Gauss' work which take these problems into account?
-
Several items in the table exhibit discontinuous rates. In (h), for example, the diagonal of the table is non
zero. Shipment within a city costs a finite amount. Often the rates form a step function - several cities at different
distances fall into the same rate class. The parcel post map shows the effect.

-
Within cities we might consider Minkowski metrics, sometimes called city block, Manhattan, or taxicab
geometries. Circles satisfying
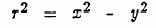 are hyperbolae, and might represent transport relations in the
vicinity of arterial road intersections. The so-called Karlsruhe metric also yields realistic isochrones for certain simiple
situations. A few empirical studies have already been done on this. Can one introduce
are hyperbolae, and might represent transport relations in the
vicinity of arterial road intersections. The so-called Karlsruhe metric also yields realistic isochrones for certain simiple
situations. A few empirical studies have already been done on this. Can one introduce
 -type weighting functions
into such geometries? The radial arterial roads from central Detroit look much like the major veins in a maple leaf, and
the isochrones resemble the overall shape of the leaf. Representation of these lines by Fourier series seems simple
enough. The minor veins in the leaf seem to satisfy Snell's law, and one can impute a friction to the parts of the leaf by
examining the angles of intersection of these veins. Similar effects seem to occur in the leaves of other botanical
species. Does this also work in the city? Certainly the finest veins visible to my eye in the leaf look very much like the
roads in a modern residential subdivision. Are similar principles at work? We also know that travel times are a function
of congestion, and this is generally directly proportional to the local population density. Thus the curvature of the space
seems to depend on the "mass" of the people. Almost everyone knows, or intuits, that the minimum travel time paths
(geodesics) from one side of the city to another are curved outward from the central business district at rush hours. Can
this be made into a general principle? Are there options other than the Minkowski, Karlsruhe, and Gaussian metrics?
-type weighting functions
into such geometries? The radial arterial roads from central Detroit look much like the major veins in a maple leaf, and
the isochrones resemble the overall shape of the leaf. Representation of these lines by Fourier series seems simple
enough. The minor veins in the leaf seem to satisfy Snell's law, and one can impute a friction to the parts of the leaf by
examining the angles of intersection of these veins. Similar effects seem to occur in the leaves of other botanical
species. Does this also work in the city? Certainly the finest veins visible to my eye in the leaf look very much like the
roads in a modern residential subdivision. Are similar principles at work? We also know that travel times are a function
of congestion, and this is generally directly proportional to the local population density. Thus the curvature of the space
seems to depend on the "mass" of the people. Almost everyone knows, or intuits, that the minimum travel time paths
(geodesics) from one side of the city to another are curved outward from the central business district at rush hours. Can
this be made into a general principle? Are there options other than the Minkowski, Karlsruhe, and Gaussian metrics?
-
In (j) the paths are very roundabout. New York to Seattle goes past Miami, then through the Panama Canal
and past San Francisco. The resulting least squares map, on which a straight line represents the travel path, is almost
inside out. There are no significant ocean routes across the N and S poles, and these places consequently go to the
outside edges of the map, as shown in the figure. Of course we know from Beltrami that only surfaces of zero curvature
can be mapped in a geodesic fashion onto a plane. But all path distances from one or two places can be simultaneously
drawn to scale on a geographical map.
The movement of people, of ideas, of technology, of disease, or of money, use complex and intricate
transportation systems. These distort our globe in profound ways. One can get from Los Angeles to Chicago, to New
York City, or to Washington, D.C., quicker than one can get to Arcata in Northern California. The airfare from Santa
Barbara to Sacramento is 107% of that from Los Angeles to New York City. By this measure Columbus, Ohio, today is
151% as far from Los Angeles as is New York, and Madison, Wisconsin, is 219% further from San Francisco than is
Milwaukee. Only a few minutes with an airline fare schedule will yield many such examples. Relations on our earth are
certainly shrinking, but they are also becoming more warped, turned inside out, and distorted almost beyond
imagination. Because of this Bunge has proposed that we use more realistic globes, with maps printed on balloons in
which well connected places are constrained by interior strings before inflation. The resulting indentations and bulges
after inflation come closer to the realities of current geography than do commercially available globes. In this
presentation I have tried to capture aspects of this new geography in terms of geometry, and it is almost possible to
believe that Euclidean geometry could not be invented by a careful observer today. Of course the world was
complicated in terms of transportation even in Euclid's day. The major modern changes, aside from speed, being
limited access air travel, railroads, highways, and electronic communication networks. These distort the simple
topology of our sphere-like earth.
Some literature:
-
Angel, S, and Hyman, G., 1976,
Urban Fields,
Pion, London, 179 pp.
-
Blumenthal, L., 1953,
Theory and Applications of Distance Geometry,
Clarendon, Oxford.
-
Bunge, W., 1966,
Theoretical Geography,
2nd ed., Lund Studies in Geography, Gleerup, Lund.
-
Dorigo, G., and Tobler, W., 1983,
"Push Pull Migration Laws",
Annals, Assn. Am. Geographers, 73(1):1-17.
-
Eisenhart, L., 1960,
A Treatise on the Differential Geometry of Curves and Surfaces,
Dover, New York.
-
Finsler, P., 1951,
Ueber Kurven and Flaechen in allgemeinen Raumen,
Birkhauser, Basel.
-
Gatrell, A., 1983,
Distance and Space: A Geographic Perspective,
Clarendon Press, Oxford, 195pp.
-
Gauss, C., 1902,
General Investigations on Curved Surfaces (1827),
Princeton University, Princeton, 127 pp.
-
Gauss, C., 1910,
"Untersuchungen ueber Gegenstaende der Hoehren Geodasie, 1844",
reprinted in Oswald's Klassiker der exacten Wissenshaften, Nr. 177, Wagrain. Leipzig.
-
Krause, E., 1975,
Taxicab Geometry,
Addison Wesley, Boston
-
Kreyszig, E., 1959,
Differential Geometry,
University of Toronto, Toronto.
-
Kumler, M., 1989,
"Directional Bias in the Ratio of Highway Distances to
Great Circle Distances Between Major Cities in the US",
Seminar paper, Geography Department, University of California, Santa Barbara, 8 pp.
-
Love, R., and Morris, J., 1972,
"Mathematical Models of Road Travel Distances",
Management Science, 25:130-139
-
Love, R., and Morris, J. 1979,
"Modeling Inter-City Road Distances by Mathematical Functions",
Operational Research Quarterly, 23:61-71.
-
Medvedkov, Y., 1965,
Ekonomgeograficheskaya Uzychennosty Raionov Kapitalisticheskogo Mira,
Prilojeniya Matematiki v Ekonomucheskoi Geografii, 2, Institute for Scientific Information, Moscow; pp. 110-120.
-
Meyhew, L., 1986,
Urban Hospital Location,
Allen & Unwin, London, 166 pp.
-
Misner, C., Thorne, K., and Wheeler, J., 1973,
Gravitation,
Freeman, San Francisco, pp. 305-309.
-
Muller, J-C., 1978,
"The Mapping of Travel Time in Edmonton, Alberta",
The Canadian Geographer, XXII(3):195-210
-
Muller, J-C., 1979,
"La Cartographie d'une Metrique Non-Euclidean: Les Distances Temps",
L'Espace Geographique, 3:116-128.
-
Muller, J-C., 1983,
"Die Nichteuklidische Darstellung Funktionaler Raume",
Kartographische Nachrichten, 33(1):10-19.
-
Muller J-C. 1984,
"Canada's Elastic Space: A Portrayal of Route and Cost Distances",
The Canadian Geographer, 18:46-62.
-
Nordbeck, S., 1964,
Framstaellning av Kartor med Hjaelp av Siffermaskiner,
(The production of Maps with the Help of Digital Computers),
Meddelanden Fran Lunds Universitets Geografiska Institution,
Avhandlingear 40, pp. 56-60.
-
Nordbeck, S., 1963,
"Comparing Distances in Road Nets",
Papers, Regional Science Assn., 12:207-220.
-
Okabe, A., Boots, B., & Sugihara, K., 1992,
Spatial Tesselations,
Wiley, New York, pp. 188-191.
-
Pieszko, H., 1970,
Multidimensional Scaling in Riemann Space,
PhD Thesis, University of Illinois, Urbana.
-
Puu, T., 1979,
The Allocation of Road Capital in Two Dimensional Space,
North Holland, Amsterdam.
-
Reichenbach, H., 1958,
The Philosophy of Space and Time,
Dover, New York, 295 pp.
-
Riemann, B., 1854,
Ueber die Hypothesen welche der Geometrie zugrunde liegen,
Dissertation, Goettingen (reprinted in Weyl, 1923, op. cit.; also in Weber, ed., 1953, Collected works of B. Riemann, Dover, New York).
-
Rund, H., 1957,
Differential Geometry of Finsler Space,
Springer, Berlin.
-
Schilling, F. 1928,
"Konstruction kuerzester Wege in einem Gelaende",
Zeitschrift fuer angewandte Mathematik und Mechanik, 8:45-68.
-
Shreider, Y., 1974,
What is Distance?,
University of Chicago Press, Chicago, 71 pp.
-
Tissot, M., 1881,
Memoire sur la Representation des Surfaces et les Projections des Cartes Geographiques,
Gautier-Villars, Paris.
-
Tobler, W., 1962,
Map Transformations of Geographic Space,
PhD thesis, University of Washington, Seattle.
-
Tobler, W., 1962,
Studies in the Geometry of Transportation,
DA-44-177-TC-685, US Army Transportation Research Command,
Northwestern University Transportation Research Center, Evanston.
-
Trunin, Y., & Serbenyuk, S., 1968,
"Maps of Accessibility in the Analysis of Economic-Geographic Space:
Cartographic Transformation of a Surface of Negative Curvature",
Voprosii Geographii, pp. 179-186 (in Russian).
-
Vaughan, R., 1987,
Urban Spatial Traffic Patterns,
Pion, London.
-
Werner, C., 1968,
"The Law of Refraction in Transportation Geography: its Multivariate Extension",
The Canadian Geographer, XII, 1:28-40.
-
Werner, C., 1985,
Spatial Transportation Modeling,
Sage, Beverly Hills.
-
Weyl, H., 1923,
Mathematische Analyse des Raumproblems,
Barcelona Lectures, Springer, Berlin (reprinted in H.Weyl, 1958,
Das Kontinum und andere Monographien, Chelsea, New York).
-
Zaustinsky, E., 1959,
Spaces with Non-Symmetric Distance,
Memoir 34, American Mathematical Society, 91 pp.
GLOBAL SPATIAL ANALYSIS
Waldo Tobler
We now have available several books on spatial analysis {Anselin 1988; Arbia 1989; Cressie 1991; Haining 1990; Gaile & Willmott 1981;
Griffith 1988, 1990; Ripley 1981, 1990; Unwin 1981, Upton & Fingleton 1985}. This is most encouraging, but is it not strange that almost none of these
works considers that the earth is homeomorphic to a sphere? The term sphere does not even occur in the index in most of these books.
This is also true of older books like {Berry & Marble 1968, and Bennett 1979}. A similar criticism applies to all the books published
in the last two decades under titles similar to "Statistics for Geographers", or "Statistical Geography", etc. This seems a most curious omission.
The same comment seems to apply to the (literally) hundreds of "Geographical Information Systems" (GIS's). The one exception,
explicitly designed to consider the spheroidal earth, is the "Hipparchus" system developed by Hrvoje Lukatela of Calgary, Alberta
{Lukatela 1987}. One other system, GIS-Plus, uses latitude and longitude for its coordinate system. Most GISs can convert from latitude and
longitude to map projections but do not treat the spherical units as their primary referencing system. And, although there has been a continued
plea for more analysis capability, most of the current GIS's do not claim to be "Geographical Analysis Systems" (GAS's). Facilitation of
analysis is the thrust of the current NCGIA initiative and I argue that this should be extended to include analysis of
global distributions.
The inference that I make from my observation is that the greatest demand is for parochial, local studies and
not for global analysis. This is inconsistent with the increased interest in global problems, especially as they relate to
the global environment, terrestrial warming, ozone depletion, and so on, and even to global economic relations. How
can this "flat earth" syndrome be overcome and round earth thinking be brought into the textbooks, mainstream
research papers and monographs, and GIS's or GAS's? Much blame must be put on the teaching of Euclidean geometry
in the elementary schools instead of the more natural earth oriented Riemann (elliptical) geometry. It is probably
hopeless to attempt to change this. Should everyone know that the circumference of a circle increases as two pi times
the sine of the radius, (which means it eventually goes to zero), and that the area of a circle increases in proportion to
the square of the sine of one half of the circular radius? Or that the circumference of a circle on the surface of an
ellipsoid depends not only on the circle's radius but also on where one puts the center {Blaschke 1949}? No one seems
to teach analytic geometry on the sphere; the most recent book which I have found is nearly 100 years old {Heger
1908}. Knowing these sorts of things would make it much easier to understand the complexities of "geographical
circles", the set of all places attainable within a given number of hours (or dollars). These circles have a circumference
bounded by isochrones (isotims), the radii are time geodesics, and the circles' shape depends on where, and when, one
begins to travel. These circles often have disjoint pieces, or holes, on the surface of the earth due to air travel. Thus
transportation systems induce a geometry even more complicated than that of a sphere or ellipsoid.
The only fields in which global analysis routinely appears are geodesy, meteorology, and oceanography,
collectively sometimes known as geophysics {Moritz 1980}. Geologists today increasingly invoke spherical ideas,
especially since the development of the theory of continental drift, and a statistican occasionally wanders into this
domain {Mardia 1972, Watson 1983}. Thus I can cite recent books such as that of {Fischer, et al. 1987, Washington &
Parkinson 1986}, and {Daley 1991}, and older ones {e.g., Chapman & Bartels 1940} that consider the geometric
nature of the earth. Generally these works are subject specific and specialized. Still they provide a starting place.
If one were to develop a course of studies introducing analysis on the earth, treated spherical, what should the
class of problems to be treated cover? One approach is to take the standard statistics book and redo the problems on a
sphere. The surface of the earth is topologically spherical, even with bumps like the Matterhorn; it is a two dimensional
manifold lacking an edge, but with some discontinuities and unsmooth derivatives, and is perhaps even fractal-like if
we don't look too closely. The boundaries above and below are of no concern so that one is immediately into two
dimensional spatial statistics (which, as Bill Bunge would remind us, neglects the danger from intercontinental
missiles). First, of course, come the two dimensional descriptive statistics, frequency histograms, density functions,
means, variances, binomials, normals, transformations, etc., all on the spherical surface. About the only idea from this
set that one routinely encounters is the population center of the United States and how it moves from census to census.
Even the few papers on centrography generally only consider planar values. Then it perhaps gets more interesting.
Scatter diagrams and correlation between observations given by latitude and longitude. We need to know how to rotate
to principal axes, a pair of orthogonal great circles (factor analysis on a sphere would need this). Or fit a "straight line",
which now becomes an arc of a great circle through a set of point locations; that is, find the pole of this great circle on
the sphere. Or does a spherical quadratic (small circle, parabola, or hyperbola), cubic, quartic, or quintic fit better? Or a
loxodrome, or some other transcendental curve? Or a nice spline, or a weighted nonparametric smooth curve? Here we
have some types of questions addressed in {Fisher et al. 1987}. Is this interesting? Do we need spherical markerboards
for the classroom demonstrations? Now move on to the analysis of spherical point patterns in the style of planar
analysis {Diggle 1983, Getis and Boots 1978}. A fleeting reference to Voronoi polygons on the sphere is found in
(Okabe, et al. 1992). Quadrat analysis must obviously be modified to become quadrilateral analysis. Or one can map
the surface of the earth into an equal area planar square {Tobler & Chen 1986} thereby distorting angles and distances,
or a conformal square {Peirce 1879} to distort areas and distances. In geology the equal area Schmidt net (known to
geographers as Lambert's {1772} azimuthal equal area map projection) and the stereographic projection are often used.
Spatial sampling takes a different form on spheres {Giacaglia & Lundquist 1972; White, Kimerling & Overton 1992}.
If we have some variable discovered or measured at point (i.e., latitude and longitude) locations we are led, inter alia, to
interpolation questions long studied in meteorology under the name of "objective analysis" {Gandin 1963; Bengtsson et
al. 1981; Thiebaux & Pedder 1987}, or "spatial analysis" {Daley 1991, p. 30}, or as "collocation" in geodesy {Moritz
& Suenkel 1978}, and recently popularized in geology and ecology as "Kriging". Most of this work is Euclidean and
planar but interpolation and contouring on a sphere has not been completely neglected {Lawson 1984a, 1984b; Renka
1984; Diggle & Fisher 1985; Willmott et al 1985} and the problem has also been approached using spherical splines
{Wahba 1981; Dierckx 1984; Hobbs 1985}. To simplify a global distribution we can do a form of trend analysis or
spatial filtering on the sphere, using spherical harmonics as the basis functions {Neumann 1838; Prey 1922; Haurwitz
& Craig 1952; Jones & Gallet 1962; Heiskanen & Moritz 1967; Balmino et al. 1973; Barraclough 1978; Colombo
1981; Tobler 1992}. Then it is also natural to ask whether the data are auto-correlated, or cross-correlated with another
variable on the earth. For analysis purposes this leads to the computation of a spectrum, and the spectra of two spherical
arrangements can be used to measure their degree of relatedness through the cross spectrum {Kaula 1967; Rayner
1971; Swarztrauber 1979}.
The usual distinctions can still be made. Some observations are measured on a nominal scale, some are
ordinal, some interval and some are ratio variables. The analyses can be parametric or nonparametric, confirmatory or
exploratory (leading to EGAS's?). The bulk of the geophysical literature treats all phenomena as fields. This means that
they exist everywhere, in space and time. Usually they consist of ratio variables that are at least piecewise continuous
and differentiable. A few odd things occur such as the piecewise continuous Ocean Function; it takes on the value one
where the surface of the earth is ocean, zero elsewhere {Munk & MacDonald 1960; Lambeck 1988}. In most of the
literature the prototypical variable is a scalar; a single number (having magnitude only) at each location. The two
dimensional topographic surface, measured as a departure from a datum, or a barometric pressure surface, are simple
examples. Beyond this are the time varying vector fields (with magnitude and direction) such as wind, or components
of terrestrial magnetism. Occasionally a field variable is a tensor; for example a matrix of strain coefficients at each
point. Another example is an anisotropic velocity surface in which a propagation velocity at a point can differ
depending on whether movement is to the north or to the south across the point, or to the east or to the west or to the
northwest, etc. In other words the traversing speed at every point depends on the direction moved at that point. A
simple instance is a freeway in which the speed along the path differs drastically from that in the perpendicular
direction (across the road). In the world of Geographic Information Systems the field variables seem to appear as
rasters, with each component of a multicomponent system considered a sample on a regular tesselation, and then stored
as a "layer". This often works well but I imagine it causes difficulty when one wants to convert to a different naming
convention such as converting from rectangular to polar coordinates, or (on a sphere), converting to an oblique pole. In
such a case a vector field does not change at all, but all of the components take on new numerical values. This means
changing the values in all the layers.
From a different point of view one can analyze point patterns on a sphere, or line patterns, or networks, or area
patterns, etc. These distinctions are made in Geographic Information Systems, but geographic analysts face problems
that are different from those that occur in geophysics. For example the Gross National Product (GNP) is a variable
defined as a spatial aggregate having meaning only for nation states. Should it be assigned as a density to all the
locations to which it applies, or should it be assigned to a point location? The first option is probably preferable since it
can then be treated as a piecewise continuous scalar. Or is it a set variable requiring a new way of thinking? Rates (of
disease incidence for example) involve comparable problems. Similarly, foreign trade data fit into a country by country
table applicable to the entire world, and as such are not representable as a simple scalar. More complex analyses are
required for such data than are necessary for the simpler scalar, vector or tensor representable phenomena. And then
there is the ill-defined problem of modifiable areal units, and the problem of data conversion between such units
{Tobler 1990}. For this problem it should be relatively simple to rewrite the pycnophylactic interpolation algorithm
{Tobler 1979} in a spherical form. Many classical geographical models relating to interaction, diffusion {Hagerstrand
1967}, migration {Dorigo and Tobler 1983}, and location also ought to be rewritten in this spherical manner. If we
look beyond statistics to include modeling then our pedagogic work ought to include the two dimensional spherical
variants of classical analysis: analytic geometry, trigonometry, vector analysis, calculus {Osserman 1977}, partial
differential (especially the diffusion and the wave) equations, finite differences, networks, transition matrices, etc. all
on the surface of a sphere (or ellipsoid). As discussed elsewhere {Tobler 1991} we really wish to use the computer
systems (GISs) as backdrops upon which to run simulations or analytical models.
The usual flat earth treatment assumes only a small portion of the sphere. Small enough that so that earth
curvature can be neglected. Then one uses flat maps on a projection chosen so that the error is not appreciable. One can
teach people how to compensate for map projection errors {Maling 1988}, but it seems easier just to forget about
working on maps. Instead, use map projections in the Transform - Solve - Invert paradigm {Kao 1967; Eves 1980}. For
example, in problems dealing with great circles it makes sense to convert from latitude and longitude to gnomonic
projection coordinates, solve the problem in these most - natural - for - the - problem coordinates, and then go back to
latitude and longitude or to a different projection for another part of the problem or, e.g., for display purposes to the
orthographic projection. The map on the gnomonic projection never needs to be seen. Mercator's projection can be used
similarly when dealing with angles in a small area, and the stereographic projection is used in meteorology because it
leaves the Laplacian invariant. The associated Legendre functions used as the orthonormal basis for the latitudinal
variation in a spherical harmonic expansion make implicit use of Lambert's equal area cylindrical map projection in this
same way {Lambert 1772; Hobson 1931}. A greater facility with spherical geometry might confine some explicit uses
of projections to these sorts of analytical transformations. Certainly the computation facilities for this are now
available. Visual displays are of course extremely important to all analytical investigations, especially exploratory ones,
and map projections are still useful for this purpose. Clearly there is a need to extend GISs to deal with and display
spherical data, i.e., we must have an Exploratory Global Analysis and Display System (EGADS). For the output of
geographical studies the systems must be capable of producing maps of the whole world.
REFERENCES
-
Anselin,L (1988): Spatial Econometrics: Methods and Models. Kluwer, Dordrecht.
-
Arbia,G (1989): Spatial Data Configuration in Statistical Analysis of Regional Economic and Related Problems. Kluwer, Dordrecht.
-
Balmino,G; Lambeck,K; Kaula,W (1973): A Spherical Harmonic Analysis of the Earth's Topography. J.G.R. 78:478-481.
-
Barraclough, D (1978), Spherical Harmonic Models of the Geomagnetic field, Institute of Geological Sciences Geomagnetic Bulletin No. 8, HMSO, London.
-
Bengtsson,L; Ghil,M; Kallen,E (Eds.) (1981): Dynamic Meteorology: Data Assimilation Methods. (Applied Mathematical Sciences, 36.) Springer Verlag, New York.
-
Berry,B; Marble,D (Eds.) (1968): Spatial Analysis. Prentice Hall, Englewood Cliffs. 512 pages.
-
Blaschke,W (1949): Kreis und Kugel. Reprint ed. Chelsea Publishing, New York. 169 pages.
-
Chapman,S; Bartels,J (1940): Geomagnetism. Oxford University Press, London; pp 549-582, 606-638.
-
Cliff,A; Ord,J (1981): Spatial Processes: Models and Applications. Pion, London.
-
Colombo,O (1981): Numerical Methods for Harmonic Analysis on the Sphere, Department of Geodetic Science Report No. 310, Columbus;140 pp.
-
Cressie,N (1991): Statistics for Spatial Data. J. Wiley, New York. 900 pages.
-
Daley,R (1991): Atmospheric Data Analysis. Cambridge University Press, Cambridge. 457 pages.
-
Dierckx,P (1984): Algorithms for Smoothing Data on the Sphere with Tensor Product Splines. Computing, 32:319-342.
-
Diggle,P (1983): Statistical Analysis of Spatial Point Patterns, New York, Academic Press.
-
Diggle,P; Fisher N (1985): Sphere - A Contouring Program for Spherical Data, Computers and Geosciences, 11,6:725-766
-
Dorigo,G; Tobler,W (1983): Push-Pull Migration Laws. Annals, A.A.G. 73(1):1-17.
-
Eves,H (1980): Great Moments in Mathematics (Before 1650). (Lecture 20: The Transform-Solve-Invert Technique) The Mathematical Association of America; 270 pages. (pp. 215-228)
-
Fisher,N; Lewis,T; Embleton,B (1987): Statistical Analysis of Spherical Data. Cambridge University Press, Cambridge.
329 pages.
-
Gaile,G; Willmott,C (Eds.) (1981): Spatial Statistics and Models. Reidel, Dordrecht. 475 pages.
-
Gandin,L (1963): Objective Analysis of Meteorological Fields. GIMIZ, Leningrad. (Department of Commerce translation, TT 65-50007)
-
Getis,A; Boots,B (1978): Models of Spatial Processes. Cambridge University Press, Cambridge.
-
Giacaglia,G; Lundqvist,C (1972): Sampling Functions for Geophysics, Smithsonian Astrophysical Observatory Special Report No. 344, Cambridge, (94 pp.)
-
Griffith,D (1988): Advanced Spatial Statistics. Kluwer, Dordrecht. 273 pages.
-
Griffith,D (Ed.) (1990): Spatial Statistics: Past, Present and Future. (Monograph No. 12) Institute of Mathematical Geography, Ann Arbor. 398 pages.
-
Hagerstrand,T (1967): Innovation Diffusion as a Spatial Process, Pred translation, Chicago University Press, Chicago
-
Haining,R (1990): Spatial Data Analysis in the Social and Environmental Sciences. Cambridge University Press, Cambridge. 409 pages.
-
Haurwitz,B; Craig,R (1952): Atmospheric Flow Patterns and their Representation by Spherical-Surface Harmonics, Geophys. Res. paper No. 14, Cambridge. (78 pp.)
-
Heger,R (1908): Analytische Geometrie auf der Kugel. Goeschen, Leipzig. 152 pages.
-
Heiskanen,W; Moritz,H (1967): Physical Geodesy. W. Freeman, San Francisco. 364 pages. pp. 251-286.
-
Hobbs,S (1985): Statistical Properties of a Nonparametric Regression Function on S^2. Ph.D. Thesis, UCSD, San Diego; 103 pages.
-
Hobson,E (1931): The Theory of Spherical and Ellipsoidal Harmonics. Cambridge Univ Press, Cambridge. 500 pages.
-
Jones,W; Gallet,R (1962): Representation of Diurnal and Geographic Variations of Ionospheric Data by Numerical Methods., J. Res. NBS 66D, No. 4 (1962);419-438.
-
Kao,R (1967): Geometric Projections in System Studies. In: Quantitative Geography. Vol. II.
(Eds: Garrison,W; Marble,D) (Studies in Geography, 14.) Geography Department, Northwestern University, Evanston;243-523.
-
Kaula,W (1967): Theory of Statistical Analysis of Data Distributed over a Sphere. Reviews of Geophysics, 1:83-107.
-
Lambeck,K (1988): Geophysical Geodesy. Clarenden Press, Oxford. 718 pages. (see p.22)
-
Lambert,J (1772): Lambert's Notes on Maps 1772. (Tobler translation 1972) (Michigan Geographical Publication No.8) Geography Department, Ann Arbor. 125 pages.
-
Lawson,L (1984a): A Piecewise CO2 Basis for Function Representation over the Surface of a Sphere, Computing Memorandum No 501; Jet Propulsion Laboratory, Pasadena.
-
Lawson,L (1984b): CO1 surface interpolation for scattered data on a sphere, Rocky Mtn. J. Math., 14(1):177-202
-
Lukatela,H (1987): Hipparchus Geopositioning Model: An Overview, Proceedings, AutoCarto 8:87-96, ASPRS & ACSM, Baltimore.
-
Maling,D (1988): Measurements from Maps. Pergamon Press, Oxford. 577 pages.
-
Mardia,K (1972): Statistics of Directional Data. Academic Press, New York.
-
Moritz,H (1980): Advanced Physical Geodesy. Wichmann, Karlsruhe. 500 pages.
-
Moritz,H; Suenkel,H (1978): Approximation Methods in Geodesy. Wichmann, Karlsruhe.
-
Munk,W; MacDonald,G (1960): The Rotation of the Earth. Cambridge University Press, London. (Appendix, pp. 287-
296.)
-
Neumann,F (1838): Ueber eine neue Eigenschaft der Laplaceschen Y(n) und ihre Anwendung zur analytischen
Darstellung derjenigen Phaenomene welche Funktionen der geographischen Laenge und Breite sind.
Schumachers Astronomishe Nachrichtungen 15:313-325. (Also in Math. Ann. 14:517-529)
-
Okabe, A., Boots, B., Sugihara, K., (1992), Spatial Tessations, Wiley, New York, pp 190-194.
-
Osserman,R (1977): Two Dimensional Calculus. Reprint ed. Krieger Publishing, Huntington. 456 pages.
-
Peirce,C (1879): A quincuncial projection of the sphere, Am. J. of Mathematics, 2(4); 394-396.
-
Prey,A (1922): Darstellung der Hoehen- und Tiefenverhaeltnisse der Erde durch eine Entwicklung nach
Kugelfunktionen bis zur 16. Ordnung. Abh., Kon. Ges. Wiss. Goett., Math.-Phys. Kl. Neu. Folge XI(1):1-29, plus
Appendix. (Translated by B. Binder as "A Mathematical Representation of the Altitude Relationships on the Surface
of the Earth, Using Spherical Functions to the 16th Order", Harvard Papers in Theoretical Geography No. 22, 62 pp, 1968.)
-
Rayner,J (1971): An Introduction to Spectral Analysis. Pion Press, London.
-
Renka,R (1984): Interpolation of data on the surface of a sphere, ACM Trans. Math. Softw., 10,4:4-7-436
-
Ripley,B (1981): Spatial Statistics. J. Wiley, New York.
-
Ripley,B (1988): Statistical Inference for Spatial Processes. Cambridge University Press, Cambridge.
-
Swarztrauber,P (1979): On the Spectral Approximation of Discrete Scalar and Vector Functions on the Sphere. SIAM J.Num.Anal., 16:934-949.
-
Thiebaux,H; Pedder,M (1987): Spatial Objective Analysis. Academic Press, London. 299 pages.
-
Tobler,W (1979): Smooth Pycnophylactic Interpolation for Geographical Regions. J.A.S.A, 74:519-530.
-
Tobler,W; Chen,Z (1986): A Quadtree for Global Information Storage, Geographical Analysis, 18(4):360-371
-
Tobler,W (1990): Frame Independent Spatial Analysis. In: Accuracy of Spatial Data Bases. (Eds: Goodchild,M; Gopal,S) Taylor & Francis, London, 115-122.
-
Tobler,W (1991): Non-Isotropic Geographic Modelling, (Presented at the NCGIA Social Science Conference, Santa Barbara, Feb 1991; Also in NCGIA TR-93-1, Feb. 1993)
-
Tobler,W (1992): Preliminary Representation of World Population by Spherical Harmonics, Proceedings of the National Academy of Sciences of the USA, 89:6262-6264.
-
Unwin,D (1981): Introductory Spatial Analysis, Methuen, London
-
Upton,G; Fingleton,B (1985): Spatial Data Analysis by Example, Wiley, Chichester.
-
Wabba,G (1981): Spline Interpolation and Smoothing on the Sphere. SIAM Journal on Scientific and Statistical Computation 2:5-16; also Errata, 3:385-386.
-
Warntz,W (1965): Macrogeography and Income Fronts. (Series Ed: Stevens,B.; Monograph Series, No 3.) Regional
Science Research Institute, Philadelphia. 117 pages.
-
Washington,W; Parkinson,C (1986): An Introduction to Three-Dimensional Climate Modeling, Oxford University Press, New York.
-
Watson, G (1983): Statistics on Spheres, J. Wiley, New York, 238 p.
-
White,D; Kimerling,J; Overton,W (1992): Cartographic and Geometric Components of a Global Sampling Design
for Environmental Monitoring, Cartography and Geographic Information Systems, 19(1):5-22.
Willmott,C; Rowe,C; Philpot, W (1985): Small-Scale Climate Maps - A Sensitivty Analysis of Some Common
Assumptions Associated with Grid-Point Interpolation and Contouring, The Am. Cartographer, 12(1):5-16
...